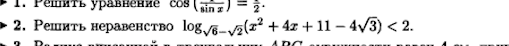Математика ЕГЭ 2023 - ч.2

Для многих детей 14 и 15 оказались сложнее остальных

Многие дети эти номера и так не умеют решать.

И не только не умеют, а природно и не смогут никогда.

Об этом и речь.

+ 10000000000000
Вот это не все понимают

Ну вы даете. Я аж полезна проверять, что это за заданий, неравенства и экономические задачи? Не путаю? Это задания как раз практически все смогут, тут никаких талантов не нужно иметь, я бы еще засомневалась по поводу геометрии.

Вы слабых детей видели когда-нибудь? А с проблемами со здоровьем? Для них 1 часть труба. Обзанимайся. Не надо на олимпиадников только ориентироваться и на хорошие школы.

Слабые дети не должны сдавать профиль и поступать туда, где нужно потом заниматься математикой.

Это Вы за них решение принимать будете? Очень удивляют теоретики. Я лично за то, чтобы как раньше было - единая математика, без деления на профиль и базу. Пусть маленькие баллы, но твои.
Меня другое удивляет. Зачем писать, то анонимно, то неанонимно. И прыгать с одного на другое.

Ну а кому нужны специалисты которые не способны даже школьную программу освоить?

Так может это проблемы программы, а не специалистов?
Работать-то все равно кому-то надо. Сильных математиков на все вакансии не хватит.

так это произойдет естественным путем - если мест в вузах будет много, то пройдут и низкобалльники - да не на все специальности не всех вузов. А уж минимальный порог, установленный вузами - согласитесь ОЧЕНЬ небольшой - на него точно и слабый школьник сдаст

Сдал ЕГЭ. Порог пересёк. Пусть учится. Не может сдать ЕГЭ, только до ОГЭ дойдёт, тоже пусть математикой занимается, хоть какие-то минимальные знания будут. И в школе должна быть математика для всех. И для слабых. Может он сегодня слабый, а завтра получше у него будет. А так можно сразу детей в утиль списывать.
Я понимаю, что правильно 1 часть в этом году обычную дали. Хоть поступят дети хоть куда-то. А дальше, не понравится учиться там (а это может быть с любым человеком и в любом ВУЗе), может всегда поменять что-то. Но шанс дан.

Ничего, что на экономику тоже профиль?!)))))

Подтверждаю. Для сына 16б и 18в были полной необходимостью. Хотя, если б дали час плюсом, то до 18й бы допер.

Неожиданностью* т9🙈🙈

да сын сказал, что ему не хватило времени на 18 задачу, хотя как решать ее он знал. и не успел сделать 13б. обидно, что не хватило именно времени, а не знаний.

Может всё-таки в другой теме будем обсуждать результаты ?или всем здесь удобно?

На соседнем форуме читала, что после началкт половина показывает ужасные результаты по математике. Это здеачи что она не освоили даже начальную школу. И дальше уже все хуже. Поэтому такие и на егэ ркзлкльаьы

Так и есть. И не только по математике.

Интересно сравнить с этим годом
В ЕГЭ по математике профильного уровня в 2022 году приняли участие 302 тысячи человек. Более 240 тысяч участников экзамена показали результаты, достаточные для поступления на инженерные, экономические и другие специальности вузов. 579 человек получили на экзамене 100 баллов.

А базу где обсуждали?

Кто там про апелляции 20 и 21 писал?
17-го уже апелляции.

Откуда вы все это берете?

Нам сказали, что выходим на апелляции 17-го

Почему 17? 19 же

Апелляция подается в течение 2-х рабочих дней с момента официального объявления результатов. Сейчас предварительно этим днем называют 19-е. Если официальное объявление будет раньше, то и дни апелляции сместятся.

В Телеге написано что эксперты проверили 2ую часть Егэ... сейчас будут обсуждать как написали все
@ExpertEgeTrenerBot

Одна проверяющая в Яндексе написала что такого давно не видела , очень плохо написали все

В яндексе написала? Это где именно?

Видимо,прямо на главной странице яндекса.

В статье Алины Акишины про Егэ математику 2023 , в комментариях посмотрите

"Сегодня завершилась проверка работ. Такого катастрофического провала не видела давно. Баллы приходилось ставить разве что за первый, чисто эмпирический пункт а) 18-й, реже за 12-ю, в единичных работах - 1 балл за 17-ю. Всё. На других позициях наблюдалась редкостная дичь, создавалось впечатление, что семи-восьмиклассник пытается наудачу нащупать ход решения задач профильного ЕГЭ.
По геометрии были лишь тщетные попытки начать решение, не более. Ни одного положительного балла на кипу работ, ни одного! Просто их не за что было начислять, хоть я всегда на стороне ученика.
Впечатление, что детей не учили математике в целом. Вообще. Очень печальное впечатление..."

Там не написано, что ужасные задания. Зато написано :"то семи-восьмиклассник пытается наудачу нащупать ход решения задач профильного ЕГЭ".

она репетитор) Ей выгодно написать, что все плохо) Уж она-то сможет подготовить. Посыл понятен

Просто ей попались такие варианты)

так она же репетитор)) Мотивация написать про все плохо очевидна

Тоже в телеге были предварительные выводы по 2-ой части. Все печально. Лучше всего решили параметры и экономическую задачу, по геометрии провал, большинство даже и не пытались

Именно к экономической задаче были основные претензии в прошлом топе.

Потому,что она долгая и отнимает много времени. Там чистая арифметика,в которой можно ошибиться.

Сложно когда дети не могут перевернуть задачу и найти другое неизвестное

Претензии из-за другого были

Параметры были хорошие,поэтому и их решили. Но многие к ним даже не готовятся,потому,что 17-18 всегда очень сложные. Наши в школе их не разбирали на подготовке даже,ибо все равно не решите. Класс ХБ. Моя готовила вторую часть с репетитором,поэтому сделала, но если бы были навороченные,то нет.

в нашей школе, а это физмат, к слову, 17 и 18 задачи тоже не готовили, потому что "время потеряете и не факт, что решите" Сын брал репетитора именно на 17 и 18 задачу, ну и 16 за одно. К сожалению 18 просто не успел физически решить, хотя сказал, что прочитав условие понял как решать.

В нашем физмате разбирали и готовили,но не все их могли решать.

мой сын, топ физмат, 18в не сделал, но репетитор, которая его к егэ готовила, сказала что и не страшно, потому что даже когда он ее решает, он ее так оформляет, что ее все равно бы не засчитали. На олимпиаде бы засчитали, а на ЕГЭ нет. Хотя вроде тренировали.

По геометрии каждый год провал

по геометрии в принципе в школах провал.
Может ее вообще убрать из расписания, заменить на алгебру? часов на нее уходит много, а на выходе это будет всего лишь одна-две задачи на ЕГЭ. При этом времени на отработку геометрия требует чуть ли не больше, чем алгебра.

Ага,а эти задачи большинство решить на ЕГЭ и не может.

Это был бы самый печальный вывод.

Какой есть. Учить геометрии лучше не станут,и понимать ее дети лучше тоже.

Почему не станут, если найти, в чем проблема? Может быть, часов как раз мало, и их надо добавить. Или найти изъяны в программе, у нас для этого есть целое Министерство просвещения.
Иначе придется вводить пропущенную геометрию в курс вузовской программы, что уже само по себе нелепо.

Проблема в задачах Егэ, в этом году были не удачные. Норм решались пункт а и все.

Может и так. Планиметрию на ЕГЭ сделать более доступной, а стереометрию оставить как есть, она всегда была задачей не для всех, "задача со звездочкой" для избранных. Интересно было бы узнать, сделает ее в этом году целиком хоть кто-нибудь.
Но не убирать же целый раздел математики из школьной программы, потому что дети ее плохо понимают...

У сына среди одноклассников есть дети, которые осилили 16 полностью, но это, действительно, способные дети, посмотрим, как это отразится в баллах ) Большинство, как и мой, только первый пункт

"Но не убирать же целый раздел математики из школьной программы, потому что дети ее плохо понимают..."
:)))
Вообще-то из вашего высказывания прямо и напрашивается, что именно убирать :)
А вообще надо вернуться к учебнику Киселева, ну и упростить курс геометрии. В обычной школе на совсем базовом уровне, в физмат классах на уровне, достаточном для инженеров в технических вузах, и хватит.

Из моего высказывание напрашивается необходимость обратить внимание на сам курс. По крайней мере, я пыталась сказать это.
Насчет Киселева поддерживаю, мои родители учились по нему, вспоминали, что геометрия была одним из любимых предметов. Что там навалял Колмогоров, и как потом создавали какие-то непонятные программы - вопрос к методологам. Если проблема видна невооруженным взглядом, она может быть решена.

Этот вопрос периодически (про учебник Киселёва) поднимается. Но только в среде преподавателей - известных математиков. И только.

сын сделал 16 задачу

Молодец, пусть все баллы зачтут! А 13-ю решал?

да, но успел сделать только А, на Б не хватило времени :(

:cool2 Он сам любит геометрию, или учитель был из любящих геометрию?

Сын любит геометрию больше алгебры, но меньше чем физику :)

А выбор его дальше какой, айти или наука? Просто любопытно:)

Попробует в ЛФИ поступить. Ели не получится даже платно, хочет хоть тушкой, хоть чучелком в мфти, куда пройдет, и все равно потом перепоступить в лфи. Да хочет физикой как наукой заниматься.

На физтехе реально с платки пейти на бюджет, также реально перевестись в другую фт школу.

на это и уповаю :)

Удачи!!!!

Спасибо :)

Добавить часов нужно МНОГО. А если учесть, что геометрия на экзамене это всего 2 задачки, в неинженерных вузах геометрия не нужна совсем, ее даже на физтехе нет, да и среди математиков многие говорят, что геометрию не понимают, то вывод напрашивается.

Геометрия на экзамене это 4 задания, не забываем про 1-ю часть. И не только будущим экзаменом определяется курс. Из матанализа в экзамене только две задачи, и то примитивные в первой части. Однако детям его дают в курсе школьной программы, и дают немало.
Это все подготовка к будущей высшей математике в вузе. В то, что на физтехе полностью игнорируют геометрию, верится с трудом. Для физиков это важный предмет.

Зачем геометрия физикам? Угол падения и угол отражения? Больше я не помню где в физике геометрия нужна. Может забыла?
Кстати, инженерам же больше черчение, чем геометрия, нужно. Вот черчение в школы вернуть, по крайней мере в физматы.

Куча чертежных программ. Зачем мучиться с этим?

Черчение для развития пространственного мышления, чтобы научиться читать чертежи, а не для того, чтобы научиться проводить правильные линии.

Как и геометрия
Основные проблемы с черчением - линии и шрифты.
Остальное - легко можно освоить.

вот и убрать линии и шрифты, оставить проекции.
Значительная часть геометрии - планиметрия, то есть не пространственное ни разу. И все задачки там на "увидеть свойство в линиях". Это требует наметанного глаза, его к этому надо долго адаптировать. Но в черчении и проекциях это не нужно и не поможет.

Геометрия изучает тела в пространстве, физика изучает материю в пространстве и времени, в пересечении вся практическая физика от механики и дальше.

Оптика. Движение по окружности. Переход к сферическим, цилиндрическим координатам. Вычисление потоков. Кристаллография...

это все имеет настолько мало отношения к школьной геометрии..
Все что вы описали можно уместить в полгода, при этом ребенок будет знать этот материал так, что от зубов отскакивать будет.

Ну, так цель школьной программы не столько знания, сколь развитие. Так, да, любой школьный предмет можно уместить в пол года. Если человек достаточно зрел для его изучения.

"Ну, так цель школьной программы не столько знания, сколь развитие."
Мы начали с того, что геометрию не осиливают даже многие математики. То есть при текущей программе развитие в этом направлении происходит очень слабое. И оно не стоит тех времязатрат, которые на него идут.

Почему вы считаете, что если человек не сумел решить навороченную задачу, то его не следовало этому пред мету обучать? Нет, если ставить главной целью сдачу ЕГЭ, то может и не следовало. А если развитие, то очень даже.

"Почему вы считаете, что если человек не сумел решить навороченную задачу, то его не следовало этому пред мету обучать?"

Я такого не говорила и не думала.

Я о другом.

Сдача ЕГЭ это измеримый результат обучения. Нравится нам это или нет. И когда вместо выпускных экзаменов нашего времени ввели ЕГЭ, все предметы, которые в ЕГЭ не попадают, моментально просели, им стали уделять внимания меньше как ученики, так и учителя. Это закон жизни: все, что не попадает в измеряемые критерии, за которые положены плюшки, начинает идти по остаточному принципу.
Если по геометрии в ЕГЭ будет всего две задачки, а по алгебре 15, при одинаковом количестве баллов за них, то здравый смысл подсказывает вкладываться в алгебру. Потому что эффект в 8 раз больше.
И только лишь осилив алгебру на максимум, браться за геометрию.
А опыт показывает, что большинство и с алгеброй имеют сложности.

Средняя школа по физике - силы. Это вектора. И сложение векторов геометрическое. Наоборот, как начинают проходить по физике силы - не хватает матем базы. Вектора в геоме в 8, а силы в физике на год раньше

Векторы это не та геометрия, которая требует многочасового набивания глаза на рисунки. Так что их как тему нужно оставить и можно дать пораньше. Тем более понятно, для чего они, и много где нужны.

Да 4 задания. 2 из которых посильны всем

На физтехе есть аналит.геометрия.

Только в ней никто не занимается геометрическими построениями. Там не будет карандаша и линейки, там не нужно уметь видеть на сложном чертеже, что вот это на самом деле равные углы, а вот это перпендикуляр.
Ну или я этого не помню.
А вот алгебра сильная нужна для этого, о чем собственно и речь. Все упирается в алгебру.

Ну, объективно, решать замудрёные тригонометрические уравнение и логарифмы тоже не особо надо. Тогда надо из всех задач убирать часть на сообразительность. Дочка тут решали испанский выпускной экзамен по математике. Там составлено именно так: если ты знаешь, что такое логарифм, то задачу с ним точно решишь. Умеешь брать производную, находить простейший интеграл, считать определитель... Т.е. программа шире нашей, но при этом никаких задач со звездочкой.

Задачи на сообразительность позволяют отобрать более сообразительных для дальнейшего их обучения.
Но если чтобы решать эти задачки, нужно потратить предварительно еще несколько сотен часов, причем в дальнейшем этот навык востребован не будет, то это просто непродуктивное использование времени людей.

Нужны ли всем подряд тригонометрия и логарифмы, это тоже вопрос. Может быть лучше для них потратить эти часы на доучивание чего-то более простого, что большинство не осиливает. Но уж тем, кто идет в физмат вузы, логарифмы явно пригодятся. А геометрия не пригодится даже им.

Не, я согласна, что вместо наших экзаменов по математике можно было бы проводить турнир по шахматам. Примерно такая же полезность...

А чем шире? Наши дети производные интегралы ведь тоже в школе проходят

В ЕГЭ у нас интегралов нет, вроде. Определителей тоже нет.

В егэ нет, а в программе (вроде про нее речь) 11 класса есть. Или не у всех?

Каких определителей? :scared2

https://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B8%D1%82%D0%B5%D0%BB%D1%8C :-)

Про матрицы, наверное.

Не изучают в школе матрицы. Или уже изучают? В мат школах на спецкурсах?

В математической школе и 30 лет назад были определители

В некоторых матшколах математику проходят более глубоко чем в вузах. но на них естественно никто не ориентируется при составлении экзаменов

Производные точно есть у всех. Интегралы и матрицы, наверное, только в профильных?

Производные и интегралы даже мы изучали в выпускных классах, это как раз начало анализа. Но у нас в экзаменах этого не было, ни в выпускных, ни в вступительных. Максимум могло попасться определение на устном экзамене в вуз. Сейчас немножко есть в ЕГЭ.

А вот матрицы в программе средней школы ранее отсутствовали вообще.

У нас в выпускном (он же мог как и вступительный засчитываться) были и производные, и интегралы, но это была профильная школа, матрицы только в спецмате, да и то очень вскользь. Сейчас простейшие производные , вроде, в первой части егэ есть? Интегралы , похоже, в общеобразовательных вообще не изучаются. Ну значит, да, прав автор поста, что в Испании программа шире, если там это не углубленка была, конечно )

Есть в егэ очень вскользь, в 1 части, на уровне понимания определения (или зазубривания). Интеграл может попасться только в виде превообразной, без упоминания понятия интеграл. Но у нас (стареньких) даже в этом виде на экзамене не присутствовало, и правильно, это задел на будущее для тех, кто дальше будет изучать математику.
Не думаю, что в Испании глубже изучают, это ничем не оправдано, интересно посмотреть варианты, предположу, что задачи типа наших из первой части - на быструю сообразительность.

Я про испанский экзамен. У них сложных задач нет, но охват по всем предметам несколько шире. Ну, и предметов больше, которые с разным весом засчитываются. Может это и более правильный подход. В принципе, для успешного обучения в вузе и прохождения вузовской программе догадываться как решить какую-то навороженную задачу по тригонометрии совсем не обязательно, а вот знать четко, что такое синус и косинус необходимо. А общий кругозор вполне можно проверить, посмотрев баллы по химии, к примеру.

Я слышу от практиков (программистов, инженеров), что геометрия в школьном виде не факт, что нужный предмет. Задачи на доп.построения теоретические, не применяются потом.

Смотря какой программист и смотря какой физик. Некоторым очень нужна

То, что где-то есть люди, кому нужна, не сомневаюсь.
Если рассматривать образование как то, что когда-то где-то может всплыть, то все не зря.
Рассматривая наше школьное образование, 95% ребят в старшей школе очень по верхам проходят как сложные геометрические задачи, так и параметры. Вот и вопрос, нормально ли это, и то, как устроен ЕГЭ

Я думаю, что нужно ещё пару задач по геометрии добавить в ЕГЭ. Причём в базу тоже. И требование по минимуму баллов по геометрии на аттестат ввести. Тогда школа научится к ним детей готовить, никуда не денется.

По русскому сочинения писать тоже очень не просто. Но без них нет аттестата, поэтому все в итоге пишут

Русским люди пользуются каждый день, на нем пишут и статьи, и постики, и научные работы. Геометрия более специфическая область знаний, плюс требует пространственного мышления, не всем дано.

Нет, просто не пытаться учить детей шаблонной математике.
Поэтому и проблемы, что дети не думают, а стараются применить знакомый шаблон. А оно не всегда работает. Вернее, почти никогда не работает в геометрии.

Выучите формулу и применяйте - с таким подходом в геометрии делать нечего

В геометрии нужны часы на то, чтобы научиться видеть рисунок, видеть в рисунке знакомые свойства и теоремы, научиться делать правильные доп.построения. Это в самом деле не работает на уровне "один раз объяснить".
Но где потом это будет нужно в жизни? Стоят ли эти времязатраты результата?

У меня тоже такое же впечатление - аналит геометрия, клоторую проходят в вузе серьезно отличается от школьной, она просто другая

Почти вся вузовская математика мало что общего имеет с школьной
Думаете, алгебра похожа на школьную?

Думаю, да.
Без умения делать сложные большие преобразования, которым обучают в школе, дальше не вытянуть ни физику, ни математику вузовскую.

Простейшие преобразования и арифметика. Предлагаете остановиться на сочетательном и распределительном законах? И достаточно

Если вы готовы решать хотя бы углубленную физику на сочетательном и распределительном законах, то останавливайтесь.

А давайте все из школьной программы выкинем? мне, например, литература в школьном варианте не нужна. Астрономия тоже, химия с биологией туда же.

30 лет назад были те же 2 урока геометрии в неделю. Но подобных провалов в геометрии почему-то не было. Может дело не только во времени?

Почему провалов? Помню, поступая в Бауманку, я тоже не смогла решить их последнюю задачу по стереометрии. И много кто не мог. Точнее, мало кто мог. Но при этом вполне решала несложные задачи на подобие треугольников и т.д. Говорит ли это о провалах? Сейчас, как я понимаю, в ЕГЭ есть только сложные задачи по геометрии. Вот если б в тестовой части были простые и их бы массово не решали, тогда б можно было говорить о пробелах. А так, нет, нельзя, в ОГЭ все несложные задачи по геометрии обязаны были решить, иначе б в 10 класс не поступили бы.

Куча двоек на огэ как раз из-за неумения решать несложные геометрические задачи, а они в первой части там совсем элементарные. И большинство не приступает к геометрии из 2 части. Откуда возьмется умение решать такое и более сложное в 11?

И в первой части ЕГЭ многие пропускают геометрию.
Вы сейчас хотите сказать, что с геометрией прекрасно, просто задачи очень сложные?)

Чтобы получить аттестат в 9 классе геометрию 2 часть можно и не решать,как в в ЭГЭ и можно получить высокие баллы.

Задача по стереометрии в ЕГЭ, как обычно, считается лёгкой. Но её мало решают. Стереометрия же.

Мой например пробниках и с репетиторами всегда решал стереометрию а на Егэ не смог (

Это и так понятно. Стереометрия сама по себе вызывает трудности у всех практически. Какие ещё усложнения её.
В пробниках иногда дают посложнее. Но на самом ЕГЭ не перебарщивают с ней.
У моего 2 года назад был максимум без двух первичных. 1 балл был снят за стереометрию и 1 в первой части. Хоть и всё расписал. Решал через декартову систему координат. Он сказал, что ему так легче.
По планиметрии во 2 части могут попадаться и усложненные задачи в вариантах в разные годы. Но с ней справляются лучше.

а как вы определяете, были провалы раньше или нет? Может у вас не было, а у соседа были?

Литература должна быть нужна не вам, она должна быть нужна (и нужна) обществу. Это, пожалуй, единственный предмет, на котором обсуждаются моральные ценности. Ну и культурные тоже.

На литературе ( у меня) надо было выучить учебник. Никаких моральных ценностей.

после 8 класса все сдавали геометрию, про массовые завалы никто не говорил, вот алгебру почему-то пересдавали

Так наверное потому и не было завалов, что был отдельный экзамен по геометрии, и ею дети занимались. Все понимали, что ее сдавать.

У нас школа проводит в 7и 8 классе годовые зачеты по геометрии, от этого понимающих и знающих не прибавилось.

Так это внутришкольные мероприятия. Если по их результатам не происходит отсева из школы, так и ладно.

А если б отсеивали,то это повлияло на знание и понимание геометрии?

Это повлияло бы на отношение детей и, что важнее, их родителей, к этому предмету и экзамену. Если они увидели бы, что ребенок не тянет, они бы впряглись сами или наняли бы репетитора. Они же ребенка старались-устраивали в эту школу и хотят, чтобы он там и дальше учился.

История тоже

+1000

Были провалы. Просто вы не видели их. В школах помогали

Да не нужны часы. Просто кому-то дано, а кому-то нет. Это как с музыкой: у кого-то слух от природы, а кому-то нужны часы упражнений, куча тренировки, и тогда он приблизится к этому результату. Ну, а кому-то медведь на ухо наступил, и как не тренирую, не напишет от диктант по сольфеджио.

Слух нельзя развить даже 1000 часов не помогаут

Геометрия обычно хуже получается у всех. Любая. Даже олимпиады, если вспомнить. На них получали призы только геометры. Кто её чувствует.

Кто убил на нее многие часы.

зависит от способностей

верю, что есть какой-нибудь вундеркинд, который мыслит геометрическими понятиями. Но обычному человеку все же нужно убить много времени. У меня с геометрией все очень хорошо было, никогда к ней плохо не относилась, но если посчитать, сколько часов мною было на одну стереометрию потрачено!... Зато решала ее в темпе записи.
А вот сейчас, 30 лет спустя, я за 2 дня воспоминаний не смогла ни одну задачу по стереометрии решить, даже самую простую. Вообще никак. Надо наверное больше времени потратить. Но на восстановление темы по физике мне достаточно пары часов.

На тригонометрию потрачено намного больше времени. И лично я ее ненавидела всегда. Но знала, и от зубов отскакивало, что не скажешь про сейчас (надо подсматривать).
Скажу вам как выпускник мехмата, не помню, чтобы она очень нужна была мне все 5 лет. А уж после диплома - вообще ни одного синуса или тангенса до тех пор, пока дети не доросли до средней школы.

Давайте не только геометрию, тригонометрию тоже выкинем. Оставим время. На что только - на таблицу умножения, может быть? Логарифмы ведь тоже в практической жизни нужны не особо.

Вы сейчас поднимаете вопросы того, что многие не работают по специальности, на которую учились.
Если бы работали, то вам, вероятно, пригодились бы логарифмы или тригонометрия. Или по крайней мере большинству выпускников.

Мой отец работает по специальности, и ему все это нужно, у него в записях сплошные логарифмы, интегралы и прочее. А вот геометрических рисунков я в его записях не видела никогда, хотя он-то как раз про разные полеты и траектории движения.

Я не поднимаю такой вопрос.
Я хочу сказать, что последовательное изучение всех разделов математики в школе расширяет восприятие информации, развивает логику и мышление. Будь то тригонометрия или конус, вписанный в шар, пересеченный двумя параллельными плоскостями.

Ну хорошо, значит я поднимаю такой вопрос :) Вы же не работаете по специальности, поэтому вам логарифмы не нужны. А вообще они очень даже нужны математикам.

Мне сейчас прислали поразвлекаться тренажер внимания. Там на экране показывают самолетики на зеленом и красном фоне. Если на зеленом, надо нажать на стрелочку, которая показывает нос самолетика, а если на красном, то хвост. И 4 направления, в которые этот самолетик может смотреть. И все это на время. То есть задача в том, чтобы быстро сообразить направление самолетика + цвет фона, и в зависимости от этого нажать указать на нос или на хвост, нажав на одну из 4 стрелочек.

Я быстро набрала 6тыс очков. А приятель, который мне это прислал, набирает 8тыс. На то, чтобы он начал набирать 8 тыс, у него ушла... пара лет! Начинал он тоже с 6тыс.
И вот вопрос. Это же тоже общее развитие, правильно? Развивает внимание и концентрацию. Нужно ли потратить 2 года на подобное развитие, и чего в этом развитии будет больше - внимания "в целом", или адаптации мозга под конкретные самолетики на зеленом и красном фоне?
И почему геометрию детям учить надо, а зеленые самолетики - не надо? в чем разница? Тем более что у самолетиков все же есть видимый прогресс, +2тыс к внимательности. А у геометрии его, зачастую, нет - дети с геометрией не дружат.

Даватйте определим, что вы подразумеваете под не дружат с геометрией.

С определением основных фигур, их свойств, площадями и периметрами дружат?
С теоремой Пифагора дружат?
С равенством, подобием - дружат?
С признаками параллельности дружат?

Все, что я написала, необходимые знания. И именно на них построены все задачи по планиметрии.
Предлагаете исключить эти знания из программы и заменить на развитие концентрации внимания, потому что оно полезнее?
Или все же научить решать задачи, используя базовые знания.

Не дружат = не любят предмет. И у детей в матшколах углубленные задачки по геометрии вызывают большие затруднения.

Что такое "дружат с теоремой Пифагора"? Знают ее и могут решить задачки на нее? Задачки в сколько действий, в одно? В одно - да. В 3 действия - уже нереально для большинства детей из обычных школ.

Задачка уровня "треугольник, в нем высота, которая делит сторону на части 3 и 4см. Вторая сторона треугольника 5 см. Найти третью сторону треугольника". И все, это уже гроб для ребенка из обычной школы. А если там еще с одной стороны будет не теорема пифагора, а угол в 30 градусов!...

"Предлагаете исключить эти знания из программы и заменить на развитие концентрации внимания, потому что оно полезнее?"
Ну а почему нет-то? Вот кто сказал, что Пифагор обязателен, а концентрация внимания - нет?
В нашей школе очень не хватает занятий по командной работе, уроков самопрезентации и публичных выступлений.. Да и машинопись сейчас бы не помешала.

Ладно, я не буду спорить.
Я сначала думала, что вы только стереометрию недолюбливаете,
но если и теорема Пифагора в вашем представлении становится лишней - я пас.

Самая простая и красивая теорема в геометрии, которая имеет тысячи применений. И если наши учителя даже к ней не могут создать интерес - что сказать. Надо убирать предмет из курса.
Уберем и посмотрим, какой будет следующим на вынос.

Я недолюбливаю стереометрию? Я ее решала в темпе записи. Она мне обеспечила поступление в вуз. Я, наверное, самый большой любитель стереометрии из всех математиков. Уверена, что из здесьприсутствующих я на нее потратила больше всего времени :))
Так что не надо на меня-то бочки катить.

Просто я не вижу смысла давать ту же стереометрию, если запланировано потратить на нее времени раз в 20 меньше, чем потратила я. Ну не будет она решаться.
Это как учить четверные прыжки в дворовой секции фигурного катания. Нет, учить можно, но их там никто и никогда не прыгнет даже близко. Хотя можно сказать что "пусть учатся для общего развития". Может для общего лучше одинарные тренировать, а? Большинство детей, умеющие кататься на коньках, и одинарные не могут. Цели надо ставить реальные.

Теорему пифагора стоит оставить :)
А еще заставить выучить всех детей длину окружности и площадь круга.
А вот без знания, что квадрат расстояния касательной равен произведению секущей.. - прекрасно проживет большинство. Особенно то большинство, которое длину окружности запомнить не может.

А у большинства учителей и не стоит задача "создать интерес"...

Блин, ну как так.. Математика уровня средних классов такая прекрасная и увлекательная, всем еще понятная, у учителя обязана быть такая задача...

Э? Ну и как вы будете увлекать хотя бы в пятом классе ребенка, которого в 4 классе недоучили банальному сложению и таблице умножения, и для него любое вычисление сродни подвигу?
А в пятом классе начинаются дроби. Весьма сложная тема, в которой даже сильные дети плавают, как показывает опыт.

В вашем изложение все настолько пессимистично звучит.. В таком случае я просто восхищена теми детьми, кто пишет профиль и набирает больше 64 баллов. Да и 64 тоже...

Так они и готовятся к этому ЕГЭ пару лет.

Математика не для всех учеников прекрасна и увлекательна. Ну равно как и любой другой предмет.

Возможно пр наличии увлечённого учителя, математика заиграла бы новыми красками. Например, в нашей школе новый учитель по обществознанию, которое мой ненавидел лютнй ненавистью. А теперь нравится, интересно.

Очень много от самого ребенка зависит - что ему нравится а что нет. Учитель не оч то и много может сделать в этом плане

.

ИМХО - тригонометрия нужна для овладения разложением функций в ряд Фурье (и наверно всякими последующими преобразованиями). А Фурье-анализ - это просто мощнейший метод, применяемый полно где в науке-технике (достаточно высокой науке-технике)

И это может тоже. Но на олимпиадах по геометрии часто и другие дети, кто на обычных не берут призы. А геометрией выбиваются.

Я в школе когда-то была в призерах олимпиад только за счет геометрии. И черчение любила. Это природное, как мне кажется.

Да. Черчение у меня плохо шло всегда..

По-моему, геометрией активно занимаются чистые математики. А, например, программисты и физики в нее вообще не углубляются, так уровень обычный углубленный. Поэтому по этим заданиям и провал.

Физиков знаю кто именно Иранскую или устную по геометрии брал.
И потом ездить то начинали когда, еще информатикой и не интересовались. Маленькие. Ну мой, например. Впустую все эти олимпиады по геометрии . Хотя геометрию в других олимпиадах делал.
А себя помню. Планиметрия ещё нормально. Стереометрия - часто правильно рисунок не могла сделать, в итоге задача решена неверно. Я стереометрию лучше видеть стала после 40-ка:)) Именно видеть. Всё остальное конечно уже утеряно.

Ещё как физики занимаются

У нас знакомый парень, с Бауманки, с ФН прикладная, математика с удовольствием помогал решать всё задачи олимпиадные, кроме геометрии.Геому сказал нет, как нибудь без меня.

На ютубе есть видео, (https://www.youtube.com/watch?v=q-3zsF090jw), как С. (некоторые здесь его фамилию с придыханием произносят), не смог решить задачку школьного этапа по планиметрии. И с этой задачкой разбирается Т.
При этом на видео С. признает, что с геометрией он не дружит. А он же крутой математик, ну и топматшкольник впридачу. А задача... ну школьный этап, не закл.
Собственно история о том, что даже явно сильные математики иногда с геометрией все же не справляются.

Все правильно, пространственное воображение мало у кого есть.

Справделиваости ради сложность не так определяется. Геометрия НЕ сложнее алгебры. А какие то конкретные стереометрические задачи сложнее каких то конкретных алгебраических
Никакой вундеркинд с матфака\мехмата\физтеха\чебышевки не докажет теорему ферма. При этом вполне себе может решить стереометрию уровня закла всеросса

+ 1

Она сложна и мало ей кто занимается

Так изначально большинство детей и расчитывать на 1 часть и 1-2 задаст из 2 части. На большее и не берутся изначальнт

Вообще, судя по тому, как устроен экзамен по математике, надо 100 балльникам ЕГЭ БВИ давать, а не олимпиадникам :) Они, получается и геометрию знают, и параметры, и олимпиадную. Да еще и трудолюбивые.

Нет уж. Олимпиадники получше подготовятся и на 100 напишут. А остальные в пролете егэшники.

Точно, подтверждать олимпы 100 баллами, а не 75

Не слишком жирно . Тогда и в вуз со 100 брать,ибо нехер. Остальнеые на платку.

Президент РФ поручил с 2024/2025 учебного года обеспечить освоение основ черчения в школах.

Как же хорошо, что моя дочь закончила школу...

Инженеры будут в приоритете.

Они всегда в приоритете. Просто наконец возвращается развитие производства а не перепродажа

где развитие производтва?! Сборка из китайских запчастей? Все разрушено, а деньги все на сво уходят(

вы бредите)

Мы в классе просили добавить черчение. Много родителей было "за". Но оно к нам в сетку уже физически не влезло, после наших многочисленных допов по математике, физике и информатике.

Давайте забудем про геометрию и разберем алгебру. Задача, которая вызвала много шума в Москве, потому что "она сложная, дети таких не решали".
Меня обвинили в прошлом топе, что я не учитель, и мне не хватает компетенций, чтобы оценивать, но я попробую.


Вот такая задача, попробую изложить алгоритм, который ни на шаг не отходит от школьной программы, от того, что дети решали:

Как решается неравенство в виде дроби, если в числителе и знаменателе переменные?

Дробь положительна, если числитель и знаменатель имеют одинаковые знаки, отрицательна, если имеют разные знаки.
Здесь есть что-то новое? Нет, неравенство в виде дроби есть в фипи, было на досроке в этом году, и это то, что совершенно точно решается в школе на уроках.

Так что без каких-то особенных знаний получаем две системы уравнений.

Числ. меньше или равен 0 и
Зн. меньше 0

Числ. больше или равен 0 и
Зн. больше 0

Решаем первую систему, видим, что знаменатель не может быть меньше 0 ни при каком Х. У данной системы решения нет. Это сложно? - нет. Это все в рамках школьного учебника и простейших задач.

Решаем вторую систему :

Видим, что Зн. всегда больше нуля с учетом ОДЗ. Находим ОДЗ.
Есть сложность? Не должно быть для тех, кто знаком с квадратными уравнениями.

Числ. больше или равен 0 - это простое логарифмическое неравенство.

Как решать любое логарифмическое неравенство - привести все к одному основанию и дальше сравнивать подлогарифмические выражения, не забыв про ОДЗ.
Переход к новому основанию делается по свойству логарифмов, которое все знают.

Все.
Где, на каком шаге возникла та самая сложность?
ВСЁ по учебнику и по фипи с его демоверсиями.

Учителя пишут, что я не понимаю, в чем здесь сложность. Я не понимаю этих учителей.

А знаменатель может быть меньше нуля?
Я уже не помню что такое логарифм, но кажется что квадрат чего угодно (если оно не мнимое), если к нему прибавить 1, меньше нуля быть не может никак. Или я условие неправильно поняла?

Не может с учетом ОДЗ. Поэтому все сводится к решению простого неравенства в числителе.

Писали в комментариях, что "это надо заметить, это сложно". Я написала обычное решение, где замечать ничего не нужно. Именно то, чему меня в свое время учили в школе. Просто решать.

Если обсуждать среднего ребенка дворовой школы, то это задание для него неподъемное.
Или про что речь?
Насколько оно сложно для детей, метящих в топ вузы?

То что знаменатель больше нуля - даже не просто неотрицательный а именно больше нуля - это должно быть достаточно элементарно для человека, планирующего поступить в вуз, где нужна математика
Выражать логарифм одного основания через логарифм другого на мой взгляд должнын аучить в школе, но в принципе и самому можно это вывести (не знаю учат этому или нет в школе)

Я в прошлом топе тоже что-то писала про это неравенство. Абсолютно согласна, что неравенство простое. Но детей научили решать шаблонно. Сначала оценить основания. А они разные! Все, разрыв шаблона, трудно, нестандартно. И еще одна "ловушка" - это то, что одно основание является произведением двух других оснований. Лезли в дебри, а посмотреть целиком на неравенство не смогли.

Я так же считаю, что стереометрия не трудная, не громоздкая, красивая.

И финансовая задача без долгих вычислений, как здесь писали.
Нормальные задания для ЕГЭ, не проще и не сложнее, чем в другие года.

Я как раз не понимаю тот шаблон, по которому детей учили, это меня и зацепило. Шаблон у меня описан. Дробь, потом оценить основания, а если основания разные, сделать их одинаковыми.

вот некоторые примеры шаблонного мышления:
- уравнение в 9 классе ( встречается во 2 части на ОГЭ) сумма квадратов двух выражений равна нулю. Выражения могут быть 4 степени. Раскрывают скобки, чертыхаются, решить не могут. а надо всего-то понять, что сумма квадратов равна 0, только если оба слагаемых равны 0. Решить не могут, трудно.
- или например финансовая задача: 1,125 возвести в 3 или 4 степень, потом умножить и разделить на что-то. И ведь сидят 1,125 в столбик умножают, потом делят, но представить 1,125 в виде дроби 9/8 не могут.
- в той же финансовой задаче не видят арифметическую прогрессию, сидят складывают подряд, даже не могут рациональным способом сложить - подряд складывают, а потом жалуются "громоздкие вычисления".
а многие ли используют формулу дискриминанта , деленного на 4 ( ну когда четный второй коэффициент) ? Нет, сидят и с большими числами вычисляют!
Что сделать? Кругозор маленький. Алгоритм знают, а целиком посмотреть на задачу и облегчить ее не могут.

Это все понимаю как раз, когда не замечают упрощения и все такое.. Ну в этой задаче именно по алгоритму надо делать в лоб, и все.. В прошлом топе писали комментарий учителя - "два раза надо было заметить". Заметить что?

Предполагаю, что во-первых заметить, что знаменатель положительный и во-вторых, что выражение в скобках - это квадрат суммы. Или , что основание в логарифме в знаменателе вообще не важно.

Опять же, предполагаю, что стали искать ОДЗ через дискриминант, дискриминант равен 0 и дальше что? Затык. Основания разные? Еще один затык. Вывод: неравенство очень сложное!

Дискрминант равный нулю не может быть затыком, это всегда подарок))

Нам с вами понятно, что это подарок, что это устно можно решать. А многие не понимают, что делать в квадратном неравенстве, если дискриминант =0.

Марс, вы если решите детей к ЕГЭ готовить, возьмите олимпиадников.. В общем тех, для кого дискриминант равный нулю будет подарком.

А кстати, в чем подарок-то?

Вы, наверное, мало задач решали по элементарной математике.
Во-первых, корень из 0 извлечь проще чем из 576, во-вторых, надо найти один ответ, а не два.

Действительно, где уж мне понять, что корень из нуля извлечь проще, чем из 576.. мне-то легче всего извлечь корень из 152 399 025. В полсекунды извлекаю :))
(шутка, если что..)

Дискриминант, равный нулю, означает вырождение двух понятных корней в один. И если с двумя дети, наверное, понимают что делать - вот правая граница, вот левая граница, серединку надо выкинуть, то когда эти две границы схлопываются в одну, у ребенка возникает резонный вопрос - а где та серединка, которую надо вырезать, и как ее обозначить? И вообще, вот эта одна точка, которая получилась (если ребенок понял, что это точка!) - ее надо выкидывать или не надо? Слишком много вопросов

Ой, все. Уже до квадратных неравенств дошли, и это сложно(((

Смотря кому. Среднему ребенку обычной школы - сложно.
Ребенку из топа - просто
Но наличие каждого подобного момента повышает уровень сложности, потому что всегда найдутся дети, которые с этим не справятся.
В приведенной вами задачке даже я 2 раза ошиблась. Сначала умудрилась не заметить, что справа ноль, и пошла переносить знаменатель в правую часть и потом смотреть на это как баран на новые ворота.. И если бы это случилось на ЕГЭ, я бы потеряла на этом минимум 15 минут.
А потом не заметила, что там X^2, и упустила отрицательные значения в решении.
То есть вот я сейчас, как есть, за эту задачу получила бы 0 баллов.

И кстати, это как раз те моменты, которые отличают данную задачку от демоверсии.

Боюсь, в демо вы допустили бы больше ошибок, там очень много преобразований. Потому что вы логарифмы не повторяли лет 10-20, к экзамену не готовились. С листа все будут долго вспоминать, что это такое.

Может я не права (не претендую на умение решать задачки 11 класса, я их 30 лет не видела, имею право глючить) но в демо я быстро избавляюсь от логарифмов (помня лишь определение логарифма) , и у меня остается что-то вроде (8x^2+7)/(x^2+x+1)>=(8x+35)/(x+5)

Ну и ОДЗ
x<>-5
(8x+35)/(x+5) > 0

Собственно все.
Оно муторно, но в таких-то вещах я не ошибаюсь. Решаю их в темпе записи, а потом еще раз пересчитываю задом наперед на отдельном листке, и если ответ сходится, значит все у меня правильно. Если не сходится, пересчитываю третий раз. На все про все минут 15

Видите, вы легко вспомнили свойство вычитания логарифмов, а переход к основанию такое же базовое (для тех, кто сейчас в школе).
Здесь замумукаешься потом все это преобразовывать, приходить к скобкам, наверное, решать методом интервалов - тоже не простота простейшая.

Да не помню я свойство вычитания логарифмов. Все что я помню - как работать со степенями. И определение логарифма.
По определению логарифма я возвела 11 в логарифм, избавилась от пугающих меня значков "log" и дальше все аккуратно преобразовала.
А то, что у логарифма можно менять основание, для меня вообще открытием стало :)) Наверное те, кто сейчас учится, об этом знают. Но в демо версии разных оснований не было. Так что встретить их это стресс. Каждый стресс это минус сколько-то пунктов "силы", которая нужна для сдачи экзамена. Иногда дети пугаются настолько, что просто не берутся за задачу, которая на самом деле была для них простой.

Вы возвели каждое основание 11 в степень в виде логарифма какого?
Я не понимаю, что вы имеете в виду. Совсем.
От значков логарифм так просто не избавишься, они потому и придуманы....

У меня было a - b >= c
Я привела это к 11^(a-b) >= 11^c

Поняла. Усложнили себе задачу) Дети знают, что разность логарифмов с одинаковым основанием это логарифм частного. И как бы вам не снизили за это балл эксперты егэ)) Хотя на апелляции можно было бы побороться.

"Поняла. Усложнили себе задачу) "

Я привела то, что я не знаю, к тому, что я знаю :))
Работать со степенями я умею, а с логарифмами нет.
Но сын на мой вопрос меня в самом деле не понял :)) Чего я хочу, зачем я пытаюсь возводить 11 в степень логарифма? :)))

Балл может и снизили бы, но к ЕГЭ бы я все же готовилась.

Но мы-то обсуждали сложность демоверсии. Так вот она не требовала от меня никаких усилий, кроме аккуратности. То есть решение не требовало включения мозга. А задача ЕГЭ меня подловила несколько раз и запутала.

С учетом знания свойств логарифма в демо версии сложнее итоговое неравенство. надо понимать метод интервалов. А в реальном просто х квадрат сравнивается с единицей.
ИМХО - равноценные они... Но вижу по реакции, что где-то был сложный момент

Я не помню никаких методов интервалов. Просто честно алгебраически решаю, аккуратно записывая все условия.

Два ограничения из свойства логарифмов - что x<>-5 и что x/x+5 > -7
И дальше два случая в основном неравенстве - если x+5 >0 и если X+5 < 0.
И никаких подвохов. Просто требуется аккуратность.
И кстати, с дискриминантом-то тоже все хорошо. Он просто отрицательный. Так что если даже его забыть посчитать, ничего страшного не случится.

У вас получится кубическая степень в знаменателе, квадратная в числителе, не уверена, что это будет просто. Хотя при должной аккуратности все решаемо системами, конечно. И что-то сократится.

зачем кубическая в знаменателе? я от знаменателя честно избавляюсь, умножая крест-накрест
a/b >= с/d = >
ad>=bc если d>0 (b там гарантировано >0)
аd<bc если d<0

В результате у меня получается кубическая как результат произведений ad и bc, но она удивительным образом сокращается с обеих сторон.
И в результате остается 12х и х^2. Если я нигде не обсчиталась. (но на егэ я бы перепроверяла обязательно)

Получили две системы неравенств.... Решается, конечно, но вы потратили недопустимое количество времени) Дети решают проще. Но вам простительно, потому что без подготовки:cool2

Я потратила 15 минут.
Я пишу преобразования не включая мозг, он мне здесь ни в какой момент не требуется.

Если дети решат еще проще - так тем более демоверсия проще, чем то, что было на ЕГЭ. Мы же об этом.

" Но в демо версии разных оснований не было. Так что встретить их это стресс." - вы понимаете, что ваша фраза и показывает ужас построения подготовки к экзаменам?

Моя фраза если что и показывает, так это мое собственное ужасное образование :)) Потому что я никакого отношения к подготовке к экзамену не имею :) Просто совсем. Я даже не знаю, как и кто к нему готовит.

Вот я увидела разные основания логарифма и пришла в ужас, потому что я не знаю, что с ними делать. А вы всегда спокойно смотрели на непонятные задачки? Или вы все и всегда решали на полный балл?

"А вы всегда спокойно смотрели на непонятные задачки? Или вы все и всегда решали на полный балл?" - нет. но и подготовка к экзаменам заключаться должна не в ожидании точно таких же заданий.

Вы же сами не решали на полный балл, значит вашей подготовки не хватало. Что удивительного в том, что и у других ее не хватает? В демоверсии был вариант 1, ученик прорешал еще варианты 2, 3 и 4, а встретился ему вариант 5, который он не тренировал.

Я и не писала, что подготовка у всех должна быть одинаковая. Это нонсенс. Конечно, она разная.
Но суть в другом.
Вы опять пишете про выданные заранее примеры.
А это тогда не про знания даже для среднего ребенка.
Плюс вы приводите в пример те моменты, которые сдающий должен уметь учитывать после курса школьной программы, просто они могут быть более кучными в каком-то примере...
А иначе пытаться писать вторую часть профиля просто не стоит.

Я вас не понимаю.
Если ребенок забыл конкретную формулу или конкретный метод - это признак его незнания математики? ему не стоит писать вторую часть профиля вообще? Этот ребенок ниже среднего?

Вот я сейчас забыла формулу смены основания у логарифма. То есть если бы я сейчас готовилась к ЕГЭ и не встретила задания на эту тему ни в каких демоверсиях, а в школе на уроках ее бы тоже упустили, я бы этот пример на ЕГЭ и не решила. Как именно это меня характеризует?

"Если ребенок забыл конкретную формулу или конкретный метод - это признак его незнания математики? ему не стоит писать вторую часть профиля вообще? Этот ребенок ниже среднего?"

Странный вывод из моего поста.
Забыл - получил меньше баллов или решил другим путем.
А вот - "Ой, а у него дискриминант равен нулю. Это пугает. А тут надо и одз помнить, и подкореное выражение, это сложно. А тут интервалы, и выколотые точки, а как же" - вот тут делать во второй части нечего. И на самои-то деле, это именно что базовые школьные вещи, просто объединенные. Да, сложнее самых простых, но и экзамен все же вступительный.

"То есть если бы я сейчас готовилась к ЕГЭ и не встретила задания на эту тему ни в каких демоверсиях, а в школе на уроках ее бы тоже упустили, я бы этот пример на ЕГЭ и не решила. Как именно это меня характеризует?"

как человека, который не может решить в силу незнания необходимого.

Почему все забывают, что в демоверсиях всех предметов черным по белому написано, что задания на тему, но не исключительно представленные...

А как вы определяете, какой материал считать базой?


Никто не забывает, что демоверсия это "не исключительно". И обычно в рамках подготовки дети решают не одну демоверсию, а много. И все равно они все "не исключительно". Но что еще дети должны сделать?

база - это знание основ разных тем, умение (попытки) применять их не только по отдельности, но и вместе.

Проблема плохих учебников, плохих учителей, излишеств на экзамене и т.п. - это уже другой вопрос.

Ну не прибедняйтесь - вывести формулу смены основания для вашего мозга это пустяк.

К примеру так . Пусть есть ЛОГаХ и ЛОГвХ . При этом в есть какая то степень а, т.е. в=а^к -> LOGaB=k
Теперь ЛОГвХ это не что иное как ЛОГ(а^k)X=1\k*ЛОГаХ . А ранее нашли 1\k=1\LOGaB -> ЛОГвХ=ЛОГаХ/LOGaB что в общем то интуитивно и понятно
(В логарифме основание я маленькой буквой обозначаю, само число - большой)

единственно что - лучше конечно заранее знать эту формулу, а не выводить ее на егэ, теряя время (это кстати к вопросу о том,что якобы нужно (для понимания) не запоминать формулы а выводить. Да это полезно, но на экзамене надо знать а не выводить. ИБО)

"Ну не прибедняйтесь - вывести формулу смены основания для вашего мозга это пустяк."

Для этого я должна была знать, что она есть. А мне это не пришло в голову. И вообще мне проще было оперировать логарифмами через степени, поэтому я смотрела в сторону возведения 15 в степень логарифма по основанию 3. Может быть на этом пути я бы к чему-то и пришла, но мне стало лень, и я пошла к сыну :)

Да

Значит среднему НЕ нужно в вуз. Делов то

Вы не заметили, что справа ноль, потом вы не заметили, что там Х^2. Это говорит о вашей невнимательности, а не об особенностях задачи.

Это говорит о том, что все мое внимание было переключено на непонятную мне вещь - что делать с разными основаниями.
Но ведь я не уникальна. Так у многих работает внимание - начинаешь думать над одним, теряешь из вида другое. Поэтому любое удивление на экзамене - потеря концентрации внимания и риск ошибок в чем-то более простом.
Вообще я ошибки по невнимательности на экзаменах и олимпиадах не делала никогда. Они у меня в принципе редки, но еще у меня достаточно методов проверки самой себя и достаточно большая скорость для того, чтобы оставалось время на проверку. Чего не скажешь, например, о моем сыне, который меняет плюс на минус на ровном месте, причем если ему сказать найти у себя ошибку - не найдет.
Поэтому если даже я делаю ошибку, я считаю что это признак проблемности задачи.

Вспомнил себя в школе - "плюс на минус" - постоянно.

Вы оцениваете задачи как человек, который не помнит логарифмы. Вы же не готовились в этом году к экзамену в отличие от выпускников, вы бы ее и не решили, конечно.

Вы думаете, все выпускники помнят формулу замены основания у логарифма? Особенно если в демоверсиях этих задач не было.
Мы же обсуждали, в чем причина сложности этой задачи. А она в том, что
а) формула сложна сама по себе, это не совсем база
б) в демоверсиях таких заданий не было, поэтому они вызывают у детей стресс.

Ну и в данной задаче еще несколько мест для того чтобы подловить ребенка. Сильный уверенный в себе и внимательный - не попадется. А чуть более слабый (каким в данном случае выступила я)- посыпется.

Откройте тему про логарифмы в учебнике, свойства логарифмов проходят на втором уроке. Задача на св-ва логарифмов может быть даже в первой части.

Вы это к чему? Хотите сказать, что сумма логарифмов и замена основания - одинакового уровня сложности?

Дискриминант появляется у детей еще при решении уравнений. В том числе и нулевой.
Это как раз все для среднего ребенка.

Да видела я, как средние дети решают квадратные уравнения..
Спрашиваешь их, как этот график называется. Они "то ли парабола, то ли гипербола... "..
Спрашиваешь, как определить, в какую сторону рога параболы смотрят - в ответ глубокая задумчивость.
Они и про линейные-то графики задумываются.
И я не знаю, как это лечить без серьезной домашки, потому что если они не набьют на это руку, они не запомнят. Завтра вспомнят, а через месяц снова будут смотреть "а что, я это когда-то знал?". При этом формулу дискриминанта как раз более-менее все помнят, даже самые слабые. На это их в школе видимо натаскивают. Но почему-то они очень не любят писать в решении уравнения значок плюс-минус. Они пишут отдельно решение с плюс дискриминантом, отдельно с минус дискриминантом. И вот если будет дискриминант 0, а у них отдельно два решения, плюс и минус, я не знаю что у них там дальше в голове случится. Но это пока не уровень моих учеников, мы такие задачки с ними не разбирали. Просто прикидываю

Вы не о средних детях пишете...

А о каких? Выше средних или ниже?
А то у меня всякие есть. Один ребенок огэ со второй попытки сдал. Другие дети в полутопах учатся.

Ниже

Дети из полутопов. Это уже выше среднего.

Ну если в полутопах такие дети, то тогда даже не знаю что и сказать.

Попробуйте подумать, какие в этих полутопах учителя, если не научили неплохих детей даже этому.

Ну и это тоже. Допускаю, что и в полутопах есть разные учителя.

Это и есть средние

Если они приучены писать два решения, то они два раза и напишут - плюс ноль и минус ноль. На пятый раз сообразят, что корень один и тот же. Это все количеством решенных задач нарабатывается.
Но, вообще, сейчас в школе не отрабатывают до механизма ?
D больше нуля, два корня, D равен нулю, один корень, D меньше нуля, нет корней.
Вот пишу и помню, как это было вбито в голову
При неравенствах добавляется так же настойчиво: а больше нуля, ветви вверх и тд

"Но, вообще, сейчас в школе не отрабатывают до механизма ?"

А у вашего сына это было отработано в школе? Если нет, то почему?

Было. По квадратным уравнениям, формулам сокращенного умножения и теории вероятностей. И теорема Пифагора. От зубов, и на этом все :( Но он учился не в России.

ясно.
Я видела отработанный материал только у одного ребенка, в 67 школе. И была в восхищении. У остальных весь процесс пущен на самотек. Им материал дали, а усвоился он или нет - уже неважно, никто не проверяет. У сильных не проверяют потому что "вы же сильные". А у слабых - видимо чтобы двоек не наставить.

История из слабой школы, как раз теорема пифагора, 8 класс. Учитель говорит, что через неделю будет самостоятельная работа, на теорему Пифагора. Дает детям демоверсию самостоятельной на дом. А потом то, что дети нарешали дома, засчитывает как самостоятельную. Видимо понимая, что если он даст что-то подобное на уроке, то придется ставить двойки столбиком.

Очень жаль..

Элана, а вы все таки репетиторствуете? или просто так, на общественных началах занимаетесь повышением общей маткультуры подрастающего поколения ? :-)

Я в качестве хобби, как начинающий, у знакомых детей средней школы.
Потому что многого я не помню, навыков пока что нет, вот пытаюсь понять что и как надо преподавать.
Началось то все с того, что был у знакомых очень слабый ребенок, тот с которым мы еле ОГЭ сдали, и денег на репетиторов у родителей не было, ребенок в 8 классе, а там даже таблица умножения на обе ноги хромает. И мы с ним все лето часов по 6 каждый день занимались. Сначала учили таблицу умножения и умножение на 100 в уме, потом закрывали пятый класс, потом прицельно уже к ОГЭ натаскивались.
У меня время тогда было.

Это 7-8 класс?

"а надо всего-то понять, что сумма квадратов равна 0, только если оба слагаемых равны 0." - вот как раз те, у кого рука набита на такой тип задач ("шаблонное мышление") - те с этим справятся быстрее. Потому что начинать раскрывать скобки - это нормально, а смотреть "а точно ли тут надо раскрывать скобки?" - требует или смекалки, или набитой на данный шаблон руки.
Когда у меня нет готового шаблона и понимания конкретного типа задач, я тоже начинаю с раскрытия скобок, и только промучившись полчаса и не найдя решения начинаю думать, не было ли другого пути (и вот здесь-то могу заметить, что можно было что-то сократить или упростить в начале).

1,125 я возводить в 4 степень в столбик не стану, по крайней мере я всегда учу не делать громоздкие вычисления до самого конца, когда станет понятно что без них никак. Сначала попытаться сократить все же.
Но вот представить 1,125 как 9/8 мне бы в голову не пришло. Это не мой метод. Скорее у меня где-нибудь в сокращении выползет 9/8. Хотя, вероятно, вы правы, и метод надо взять на заметку.
А можно саму задачку посмотреть, как она может выглядеть?

- не видят арифметическую прогрессию? А ребенок какого уровня? Топ мат наверное увидит. Средний ребенок полутопа скорее не увидит. Это сложно. И опять-таки, как раз увидеть - это про набитость руки/глаза на подобные вещи, то есть про натасканность. Если он эту арифметическую прогрессию последний раз видел в листочке за пятый класс, то и упустит.

По идее, одна из задач учителя (репетитора) и объяснить ребенку разные варианты - то есть обязательно научить первым делом проверять разложение/сокращение/иное представление.
И если этого не делают, то дело не в том, что ребенок средний - ему, бедняге, просто никто не объяснил.

"а надо всего-то понять, что сумма квадратов равна 0, только если оба слагаемых равны 0." - вот как раз те, у кого рука набита на такой тип задач ("шаблонное мышление" ) - те с этим справятся быстрее.
- это не шаблонное мышление, это ОСНОВА.

Ужас, если так пишут и думают те, кто готовят детей.

Основа ожидать в первой попавшейся задачке, что она будет на что-то раскладываться или что это будет сумма квадратов, каждый из которых должен быть равен 0? По-моему, это как раз шаблон.
Шаг 1. Проверить, не относится ли задачка к типу "сумма четных степеней равна нулю, значит каждое из слагаемых равно 0".
Если нет, переходим к шагу 2.
Шаг 2. Смотрим, нельзя ли заметить общие множители, которые можно сократить. Замечаем, сокращаем. Не забываем выписать отдельно неравенство нулю того, на что сократили.
Если сокращать нечего, переходим к шагу номер 3.
Шаг 3. Раскрываем скобки.

Наверное вы правы, так будет продуктивнее для детей. Возьму на заметку. Но лично я сама так не делаю.

"Основа ожидать в первой попавшейся задачке, что она будет на что-то раскладываться или что это будет сумма квадратов, каждый из которых должен быть равен 0? " - ну не так буквально, но в целом.

знаете, это как один учитель тупо из параграфа учебника предложения повторяет и формулы на доске пишет - а дальше проверяет не свой вклад в ученика,
а другой:
умеет объяснить, разжевать, переспросить;
увидеть слабые стороны после контрольной и обязательно вернуться к ним;
покажет несколько решений (ну где они возможны);
а еще обучит маленьким хитростям для облегчения счета ну и алгоритму, да

первого гнать надо (а их большинство, к сожалению), вторые - умницы, но редки стали

На мой взгляд научить ребенка правильно считать - это обучение.
Набить руку на то, чтобы он замечал, когда в задачке есть сумма четных степеней и приравнивать их к нулю - это тоже обучение. Учить видеть.
Дать ребенку последовательность "сначала проверьте четные степени, потом попробуйте разложить на множители, если не получится множители - попробуйте выделить полный квадрат, а если и он не получится - тогда раскрывайте скобки" - это уже все-таки шаблон. И он подстраивается под конкретный экзамен, в зависимости от частоты определенных задач.

Это не шаблон в целом, а то самое умение видеть, упрощать и решать. Ну и вы не воспринимайте столь буквально, что такое для каждого задания.

Мой личный опыт показывает, что иногда я не вижу. Оно же тоже не прямо на поверхности, обычно запрятано где-то, то есть не всегда сразу увидишь. Поэтому идти одним путем, потом останавливаться и искать другой путь - это нормально.

9/8 или 1,125 встречается в финансовых задачах, где процентная ставка 12,5%. Можно много таких задач найти. Например, на сайте "решу ЕГЭ".

Арифметическую прогрессию не видят. Это очень плохо. Ладно, без формул прогрессии. Но такие дети даже сложить или умножить рационально не могут. Она умножают, складывают подряд. В каком порядке написано, так подряд и складывают. Или умножают. Потом говорят, что времени не хватило.
Вы можете устно найти сумму чисел , например, от 1 до 100? Конечно. Мы знаем, что сумма первого и последнего слагаемого 101, а также сумма второго с начала и второго с конца тоже 101. Всего 50 пар таких сумм по 101. Всего 5050. А многие будут складывать подряд, потратят кучу времени. Это не шаблон.
Такие хитрые моменты в каждой задаче можно найти, которые упрощают задачи и помогают избежать длинных вычислений.
Кто может увидеть, применить и успеть сделать все , тот и получит больше баллов. Так и должно быть. Иначе как дифференцировать учеников, если дать лёгкие задачи и все получат по 100 баллов.

"9/8 или 1,125 встречается в финансовых задачах, где процентная ставка 12,5%. Можно много таких задач найти. Например, на сайте "решу ЕГЭ"."

Ок, посмотрю, спасибо.

".... Мы знаем, что сумма первого и последнего слагаемого 101, ....А многие будут складывать подряд, потратят кучу времени. Это не шаблон."

Тут ключевое, что мы ЗНАЕМ. Мы не сами изобрели этот метод, нам его показали в детстве, и давали немало задач, где он применяется. Как правило на олмате. То есть моя дочка с олматом это моментально видит, не единожды наблюдала это у нее. А вот увидит ли это другая девочка из полутопа, у которой нет олмата - я спрошу в ближайшее время, очень интересно, кстати. Допускаю, что нет.

Сумму 1 и 100 я привела для примера. Как вы будете складывать другие числа, если они не представляют прогрессию. Подряд? Или выберете удобные, которые при сложении дают в конце 0, ну или ещё что-то сами увидите. А если положительные и отрицательные вперемешку. Конечно, не подряд, а рационально. В любом учебнике есть такие задания " вычисли наиболее рациональным способом". Но все равно, многие не помнят, не хотят запоминать и применять. Легче жаловаться, что это трудно. А родители подпевают.

В задачнике 57 школы есть несколько больших глав на вот такие удобные вычисления, их там специально отрабатывают. В обычных школах этим не занимаются.
Кстати, в тренажерах Некина тоже эти задания были, например вот:

Из двух примеров решить наиболее легкий
(1) 663 + 86 + (643 − 4) =
(2) 663 + 86 − (643 − 4) =

Вот целая подборка, и там еще есть скрипты для генерации подобных листов:
https://nekin.info/math/xrc/080/080006_3dejstvija_porjadok.pdf
Ну и разная сложность тоже.
И я их с детьми отрабатываю, потому что вижу, что их этому не учат.
Но вот арифметическую прогрессию проходить не приходило в голову, учту.

Только знаете... вот все эти темы дети должны бы отрабатывать классе в пятом-шестом, а многое так и вовсе в четвертом. Поэтому я сейчас и считаю, что брать репетитора надо уже классе в пятом, чтобы хотя бы вот этот счет автоматизировать, научить ребенка считать правильно. Потом уже не успеть.

Так суть в том, что такие вещи не на олмате должны давать, а всем в любой школе

Методы оптимального счета есть в учебниках? В каких?

Методов оптимального счета много. Например, переместительный закон сложения или умножения. Переставил слагаемые нужным образом и посчитал. Или сначала сложи все положительные слагаемые, потом все отрицательные и только потом окончательный вариант. Или распределительный закон умножения ( в ОГЭ в задачах про шины часто такое есть), вычислить сумму и разность сложного выражения, где можно что-то вынести за скобку и счёт практически устный. Или в уравнениях не торопиться умножать, часто потом придется это произведение на что-то делить, проще сократить. Или представить десятичную дробь в виде обыкновенной, все сокращается и умножить можно устно , как в примере с 9/8)
Если начать отрабатывать оптимальный счёт, то на другие темы не останется времени.

Пишу сейчас и вспоминаю учеников, которые на 100 умножают столбиком. Или делят. Или что-то подобное. Им говоришь, как проще, а у них взрыв мозга - не по силам им это. А потом они собираются профиль математику сдавать.

А вообще это обширная тема для обсуждения. Моё субьективное мнение, что сначала надо научить детей сложению, умножению, всему тому, что в начальной школе, а потом уже начинается вся красота математики. А у нас погоня за " чем раньше, тем лучше" приводит к тому, что школьники к 5 классу уставшие, легче списать, чем думать, или жаловаться, что трудно.

Вот знаете, прямо по теме этой беседы.
Хороший ребенок, все задачи решает в 2 счета, учится в топе, арифметическую прогрессию знает.
Но умножает на 5 столбиком, и 99*3 это 11*27 или как-то так.
Думаю, просто ему такую идею никто не подкинул.
Многие вещи нам непонятны не потому, что наши понятия слабы; но потому, что они не входят в круг наших понятий.
А может он прикалывался специально?...


А в задачнике 57 школы отрабатывают все упомянутые методы счета. То есть они успевают это сделать.
На самом деле многие вещи отрабатываются в домашке, а домашку можно сделать любого объема. Но вот у моего ребенка домашки вообще нет. Не видела я, чтобы моя над алгеброй дома сидела. Геометрия была в прошлом году, в этом и ее нет. Ну и результаты сразу намного хуже.

Я учила умножать на 100 в уме ребенка, который пересдавал ОГЭ. И у него это получилось и достаточно быстро.

" Моё субьективное мнение, что сначала надо научить детей сложению, умножению, всему тому, что в начальной школе, а потом уже начинается вся красота математики"
Согласна. И это - началка, в которой это недоучивают. А народ гонится за Петерсон и 1-3.

Меня тут опередили с ответом - тех, о которых я говорю, напрямую, наверное и нет, но на то и учитель с репетитором...

А в задачнике 57 школы -есть.

Ну а причем тут свой задачник конкретной школы?

Просто что они считают нужным уделить этому отдельное внимание, в рамках школы.

ну уж если даже в матклассах таких это не давать, то...

это обычные общеобразовательные классы 57 школы.
в матклассах это давать странно. сильные дети обычно как-то сами этим владеют. (если речь про 8 и старше)

Шаблоно учат всех детей. Иначе результат ещё хуже будет. Не всем дано

После слов " знаменатель меньше или РАВЕН нулю" дальнейшие рассуждения мадам, желающей стать репетитором, можно не читать.

Поправила, спасибо, копипастом увлеклась, не заметила.
По теме можете сказать, что именно оказалось сложным в этом неравенстве?

Мне? Мне ничего.
Добавлю...
Большинству моих детей из классов, где я преподаю, тоже.

Давайте я скажу.
Во-первых, увидев что знаменатель не может быть отрицательным, легко забыть, что там еще нужно учесть область допустимых значений. Большой соблазн знаменатель просто откинуть, соответственно забыть учесть ОДЗ

Во-вторых, смена оснований это уже не для среднего ребенка. Хотя мой вроде формулу знает, наверное в этом не ошибся. А вот откинуть знаменатель мог запросто, внимательность у моего пониженная.

В-третьих, когда переходишь к работе с числителем, там в обоих частях неравенства появляется что-нибудь типа log15 X2, и велик соблазн его сократить и тоже забыть. А надо учесть, что если он отрицательный, то знак у неравенства надо перевернуть. Короче, не должен он отрицательным быть.

В общем, 3 таких подвоха, мощных. Превращающих задачу в задачу для очень продвинутых и внимательных.

Есть еще микроподвох номер 4. У знаменателя дискриминант равен 0. Надо сообразить, что именно с этим делать, и как записать пересечение этого множества с множеством значений, полученных из числителя. Это макро-подвох номер 5.

Марс, вы вроде говорили, что у вас сын средне ЕГЭ писал. или я ошибаюсь? Если средне, то просто дайте ему эту задачу и посмотрите, как он сам ее решит. И все косяки словите.

Не Марс.
Поясните, что вы имеете в виду " когда переходишь к работе с числителем, там в обоих частях неравенства появляется что-нибудь типа log15 X2, и велик соблазн его сократить и тоже забыть."
1. как в числителе получается основание 15?
2.что такое обои (обе) части неравенства? Это когда справа ноль, что ли? или как?
3. ....."не должен он отрицательным быть".....Никакой знак неравенства не меняется. Вы о чем? Поясните.

1. А, ну это я как типичный дурак, который все что помнит про логарифм - это его определение, и открывший для себя формулу замены основания логарифма, пошла сравнивать логарифм по основанию 3 и логарифм по основанию 5 через приведение их к основанию 15, то есть каждый из них привела к дроби, где в числителе оказался логарифм x^2 по основанию 15.
В результате-то у меня получилось то же самое, что у сына (дала ему сейчас эту задачку решить), только он сразу сообразил, что x должно быть >=1, а я вот через эти дроби. Это как раз разница между человеком, у которого набита рука, и тем, кто пытается на месте сообразить, что с этим делают.

Кстати, вот еще один подвох, на котором можно попасться (и я попалась) - что там же X^2, а не X, а значит в решении будут не только >=1, но и <=-1. Я об этом забыла, считала что там X (все мои мозговые ресурсы ушли на воспоминания про логарифмы... Я их первый раз за 30 лет вижу).
При этом на правом диапазоне надо еще не забыть выколоть точку из ОДЗ знаменателя. А на левом диапазоне - не надо.

2. Это туда же, выше. Неравенство между двумя логарифмами числителя.
log3(X^2)>=log5(X^2)

Вы меня сейчас пугаете)) Квадратные уравнения выпадают в трети заданий ЕГЭ, дикрминант равный нулю не является чем то особенным, как и дискриминант отрицательный. Это отработано хотя бы в разделе изучения парабол (не говоря уж про изучение кв уравнений).

Что касается соблазнов "сократить" Log - это делается во всех логарифмических неравенствах. Переход к сравнению подлогарифмических выражений. Так оно решается, Чем именно это неравенство стало сложным по сравнению со всеми другими?

Про ОДЗ просто промолчу.

Я не спросила, почему оно сложное. Вопрос был - чем оно сложнее других, хотя бы того, которое было в демо версии? Там, обратите внимание, с дискриминантом тоже "не все идеально"))))

в демоверсии хотя бы основание одинаковое, уже легче.
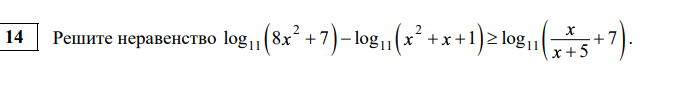
И знаменателя никакого нет.
И нет соблазна откинуть знаменатель, забыв учесть у него ОДЗ.

То есть эта задача имеет на 3 уровня сложности меньше, чем приведенная вами
(хотя может у нее еще какие-то подвохи есть, ее надо решить чтобы их поймать)

В демо версии для ОДЗ четыре ограничения, это еще сложнее, если уж вы это считаете подвохом:).

А переход к другому основанию это свойство логарифма . Вы не сможете решить демо неравенство, не зная свойств логарифмов.

В чем разница? Демо более громоздкое, решается дольше.

"А переход к другому основанию это свойство логарифма . Вы не сможете решить демо неравенство, не зная свойств логарифмов."

Я просто возвожу 11 в степень логарифма. Я помню свойства степеней.
Что 11^(a-b)= 11^a/11^b.
Этого не достаточно для решения демо-варианта?

У вас в условии разность логарифмов. Что вы возводите в степень? Не поняла

"И нет соблазна откинуть знаменатель, забыв учесть у него ОДЗ." - ну так можно дойти до того, что и уравнения по школьной программе решать не надо, а то там тоже такой соблазн бывает

Сложно вам будет репетитором быть...
Что же ваш ребёнок только первую часть решил и то со второго раза.... все же легко...
Если вы не можете спуститься на уровень детей, то поверьте школьным учителям....они как раз могут.

Так ее ребёнок и не в России учился.
Это первое. Второе. Есть дети которые на 1 и способны только и это успех